The index function returns the position of an item in a list. The function takes up to three parameters. One of them is required and the other two are optional.
|
1 2 |
numbers = ['one', 'two', 'three'] print(numbers.index('two')) |
Objects in Python are zero-index, so the indexing starts from 0. If you run the code, the above code returns 1 as an index of the list.
The first position of an item
The values in the list from the previous example are unique. You can add another element that’s a duplicate.
|
1 2 |
numbers = ['one', 'two', 'three', 'two'] print(numbers.index('two')) |
Now, you have two “two” values. If you run the code, it will return the index of the first element, so the result will be the same as before.
1
The last position of an item
The index function looks for the value from the beginning of a list. If you want to iterate over a list from the end to the beginning, you have to reverse elements in the list. You can do that by using the reverse function.
|
1 2 3 |
numbers = ['one', 'two', 'three', 'two'] numbers.reverse() print(numbers.index('two')) |
Using only the reverse function will give us 0 as the result, so it’s not exactly what we expected. We have to do some math.
|
1 2 3 |
numbers = ['one', 'two', 'three', 'two'] numbers.reverse() print(len(numbers) - numbers.index('two') - 1) |
Let’s take a look at the result inside the print function.
There are 4 elements in the list. From this number, we subtract the index of the reversed list, which is 0. This will give us 4. Because indexing starts from 0 and not 1, we have to subtract one to get the index of the last “two” elements.
3
All positions of an item
The index function iterates through the list until it finds the matching element. When it finds it, it stops. If you want to find all matching elements, you can use the list comprehension and the enumerate function.
|
1 2 3 |
numbers = ['one', 'two', 'three', 'two'] indexes = [i for i, x in enumerate(numbers) if x == 'two'] print(indexes) |
This code will print a list of indexes. In our case, there are two.
[1, 3]
If you want, you can do it in a single line.
|
1 |
print([i for i, x in enumerate(['one', 'two', 'three', 'two']) if x == 'two']) |
Handle exceptions if there is no item
So far, we have dealt with lists that contain at least one matching item. Let’s see what’s going to happen if there is no such element inside the list.
|
1 2 |
numbers = ['one', 'two', 'three', 'four'] print(numbers.index('five')) |
If you run this code, Python is going to raise an error.
ValueError: 'five' is not in list
There are two ways we can deal with it.
Check if there is an element inside the list
There are a few approaches you can use to check if the specified value is inside a list. Probably the most “pythonic” way to do it is to use the “in” word.
|
1 2 3 4 5 6 |
numbers = ['one', 'two', 'three', 'four'] value = 'five' if value in numbers: print(numbers.index(value)) |
This code returns nothing because there is no “five” inside the list.
Handle exception using try .. except
Another way to handle the exception is to use try .. except.
|
1 2 3 4 5 6 |
numbers = ['one', 'two', 'three', 'four'] try: print(numbers.index('five')) except ValueError: print('No such value in the list!') |
In this case, there is no “five” inside the list, so Python returns code under except clause.
No such value in the list!
Checking the x number of items
At the beginning of the tutorial, I wrote that the index function takes two optional parameters.
The index function checks every element of a list until it finds a match. If we are using long lists that can take a lot of time.
Take a look at this example. This code searches the entire list for a match.
|
1 2 |
numbers = [*range(1_000_000)] print(numbers.index(999_999)) |
It has to iterate almost the entire list to find a match. If you can estimate where Python should search for the value, you can lower the time needed to do this operation.
|
1 2 |
numbers = [*range(1_000_000)] print(numbers.index(999_999, 900_000, 1_000_000)) |
The search starts from 900,000, instead of 0. This results in reducing the operation by about 10x.
Of course, for such small numbers, it’s hard to see which one is actually faster. We can quickly use the timeit module to check the execution time of small bits of code.
|
1 2 3 4 |
from timeit import timeit print(timeit('numbers.index(999_999)', setup='numbers = list(range(1_000_000))', number=1000)) print(timeit('numbers.index(999_999, 900_000, 1_000_000)', setup='numbers = list(range(1_000_000))', number=1000)) |
The last parameter tells the interpreter how many times the code should be executed. In our case, it’s 1000 times.
If you run it, you’ll see that the second part of the code is executed approximately 10 times faster than the first one.
11.836976 1.1330223000000004
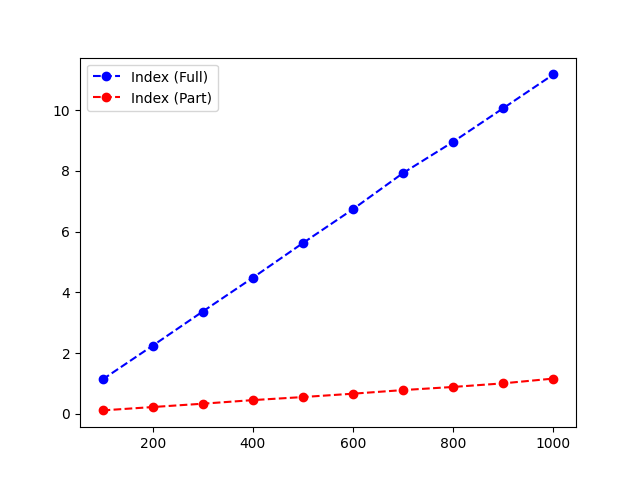
Let’s create a benchmark where we can see these numbers for multiple different values and display them inside a chart. To draw a chart we are going to use the matplotlib module.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
from timeit import timeit import matplotlib.pyplot as plt numbers = [] full_range = [] part_range = [] for i in range(100, 1001, 100): numbers.append(i) full_range.append(timeit('numbers.index(999_999)', setup='numbers = list(range(1_000_000))', number=i)) part_range.append(timeit('numbers.index(999_999, 900_000, 1_000_000)', setup='numbers = list(range(1_000_000))', number=i)) fig, ax = plt.subplots() ax.plot(numbers, full_range, '--bo') ax.plot(numbers, part_range, '--ro') print(full_range) print(part_range) plt.show() |
This code is run inside a loop for 100, 200, …, 1000 times. Take a look at how much time each iteration took for different numbers.
| Number | Index (Full) | Index (Part) |
| 100 | 1.12 | 0.11 |
| 200 | 2.24 | 0.22 |
| 300 | 3.36 | 0.33 |
| 400 | 4.48 | 0.45 |
| 500 | 5.63 | 0.55 |
| 600 | 6.74 | 0.66 |
| 700 | 7.93 | 0.78 |
| 800 | 8.96 | 0.88 |
| 900 | 10.07 | 1.00 |
| 1000 | 11.18 | 1.16 |
At the end of the code, the show function displays the chart.
Using NumPy
NumPy adds support for large multi-dimensional arrays. This library can also be used to find an index in a Python list.
|
1 2 3 4 |
import numpy as np numbers = ['one', 'two', 'three', 'two'] print(np.where(np.array(numbers) == 'two')[0][0]) |
The returned index equals 1, as the first matching value is in the second position. The list number is converted to the NumPy array.
You can easily modify it to return all matching positions.
|
1 2 3 4 |
import numpy as np numbers = ['one', 'two', 'three', 'two'] print(np.where(np.array(numbers) == 'two')[0]) |
Now, index 1 and 3 is returned.
[1 3]
Using Pandas
Another popular library for data manipulation is Pandas. This code displays the first matching index.
|
1 2 3 4 5 6 |
import pandas as pd numbers = ['one', 'two', 'three', 'two'] series = pd.Series(numbers) print(list(series[series == 'two'].index)[0]) |
If you want to return all matching indexes, remove [0] from the last line of the code.
Benchmark
For simple examples, it doesn’t matter which form you are using to find indexes, but it makes a huge difference for a big number of calculations or big data.
That’s why I wanted to show the differences between these three methods: index function, NumPy, and Pandas.
Run this code to get a list of values and a chart.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
from timeit import timeit import matplotlib.pyplot as plt numbers = [] full_range = [] numpy_range = [] pandas_range = [] for i in range(100, 1001, 100): numbers.append(i) full_range.append(timeit('numbers.index(999_999)', setup='numbers = list(range(1_000_000))', number=i)) numpy_range.append(timeit('np.where(np_array == 999_999)[0][0]', setup='import numpy as np\nnumbers = list(range(1_000_000))\nnp_array = np.array(numbers)', number=i)) pandas_range.append(timeit('series[series == 999_999].index[0]', setup='import pandas as pd\nnumbers = list(range(1_000_000))\nseries = pd.Series(numbers)', number=i)) fig, ax = plt.subplots() ax.plot(numbers, full_range, '--bo', label='Index (Full)') ax.plot(numbers, numpy_range, '--yo', label='NumPy') ax.plot(numbers, pandas_range, '--go', label='Pandas') print(full_range) print(numpy_range) print(pandas_range) plt.legend() plt.show() |
Let’s take a look at how the data looks inside a table.
| Number | Index (Full) | NumPy | Pandas |
| 100 | 1.12 | 0.09 | 0.11 |
| 200 | 2.26 | 0.10 | 0.23 |
| 300 | 3.34 | 0.16 | 0.33 |
| 400 | 4.49 | 0.21 | 0.45 |
| 500 | 5.59 | 0.26 | 0.54 |
| 600 | 6.66 | 0.33 | 0.67 |
| 700 | 7.82 | 0.37 | 0.78 |
| 800 | 9.02 | 0.43 | 0.89 |
| 900 | 10.05 | 0.48 | 0.99 |
| 1000 | 11.15 | 0.53 | 1.11 |
It will be easier to visualize that using a chart.
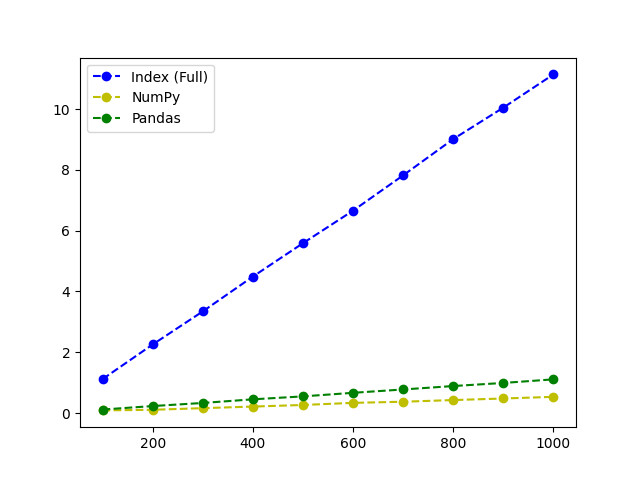
You can see that both NumPy and Pandas are much quicker than the standard index function. In this case, NumPy is the quickest way (20x) as it works great with smaller data sets.